GBA Programming - Decimals and Matrices
2021-03-15
After getting objects working, I want to also work out how to get affine transformations working. This will allow me to rotate and scale my sprites.
Switching on affine transformations
Looking at the documentation, the OAM entry takes on a slightly different form when the affine bit it turned on. Lets make a struct for it:
struct oam_affine {
/* 0-7 */ unsigned int y : 8;
/* TRUE*/ bool affine_enabled : 1;
/* 9 */ bool double_size_enabled : 1;
/*10-11*/ enum OBJ_MODE mode : 2;
/* 12 */ bool mosaic_enabled : 1;
/* 13 */ bool palette_256 : 1;
/*14-15*/ enum OBJ_SHAPE shape : 2;
/* 0-8 */ unsigned int x : 9;
/* 9-13*/ unsigned int affine_param_index : 5;
/*14-15*/ enum OBJ_SIZE size : 2;
/* 0-9 */ unsigned int tile : 10;
/*10-11*/ unsigned int priority : 2;
/*12-15*/ unsigned int pallette : 4;
unsigned int __affine_param_space : 16;
} PK_AL(4);
const struct oam_affine oam_affine_zero = {
.affine_enabled = 1,
};
Changing nothing else, I could tell that something was wrong when I turned affine transformations on:
From Tonc:
"When flagging a background or object as affine, you must enter at least some values into pa-pd. Remember that these are zeroed out by default. A zero-offset means it'll use the first pixel for the whole thing. If you get a single-colored background or sprite, this is probably why. To avoid this, set P to the identity matrix or any other non-zero matrix."
Well there we go then. At the end of each OAM entry, there are 16 bits spare. 4 of those spaces make up one entry into the affine transformation table, with variables PA, PB, PC and PD spread across those spaces.
0x07000000 ┐
0x07000002 ├─ OAM Entry 0
0x07000004 ┘
0x07000006 ── PA in Affine Entry 0
0x07000008 ┐
0x0700000a ├─ OAM Entry 1
0x0700000c ┘
0x0700000e ── PB in Affine Entry 0
0x07000010 ┐
0x07000012 ├─ OAM Entry 2
0x07000014 ┘
0x07000016 ── PC in Affine Entry 0
0x07000018 ┐
0x0700001a ├─ OAM Entry 3
0x0700001c ┘
0x0700001e ── PD in Affine Entry 0
... repeat x32
The affine_param_index variable in OAM is used to index into this table so the GBA knows which affine parameters to use for this sprite. Because these entries are all 0s by default, the sprite isn't displaying correctly.
I needed to set these value to an identify matrix, like so:
struct oam_affine_param {
u16 __filler1[3];
s16 pa;
u16 __filler2[3];
s16 pb;
u16 __filler3[3];
s16 pc;
u16 __filler4[3];
s16 pd;
} PK_AL(4);
volatile struct oam_affine_param* main_affine = GetOAMAffinePointer(0);
// These are fixed point numbers, soon to be worked out
main_affine->pa = main_affine->pd = 1<<8;
main_affine->pb = main_affine->pc = 0;
With these set, my arrow displayed correctly. After that I moved onto actually working out how affine transformations work on the GBA.
Fixed point decimals
Unlike modern system, the GBA's teeny ARM7TDMI does not have a floating-point unit. Whenever I use floats or doubles in my code, my compiler is subbing in code to handle these decimals manually, which means it's very slow.
The GBA has its own system to handle decimals, the more primitive fixed-point numbers. These work exactly like a signed integer, except they are treated as if there is a decimal point. The 16-bit fixed-point numbers used in the affine table are in 8.8 format, so 8 integer bits before the decimal, and 8 fractional bits after the decimal.
This means its very easy to convert from ints to fixed-point decimals, I just shift 8 bits to the left. That's what the 1<<8 was earlier.
After finding out that the GBATEK documentation was wrong (the fixed point numbers don't use a sign bit, they use two's compliment like regular signed ints), I followed Tonc again for guidance on their implementation.
Adding and subtracting fixed-point numbers just works, but for multiplication/division they need to be shifted along to account for the decimal point moving.
#pragma once
#include <gba_types.h>
#include "macros.h"
// GBA 8.8 Fixed point decimal format
// Used https://www.coranac.com/tonc/text/fixed.htm#sec-fmath
// to help with conversion functions.
typedef s32 fixed32;
typedef s16 fixed16;
#define FIX_SHIFT 8
#define FIX_SCALE 256
#define FIX_SCALEF 256.0f
static inline fixed32 fx_from_int(int d) {
return d << FIX_SHIFT;
}
static inline fixed32 fx_from_float(float f) {
return (fixed32)(f*FIX_SCALE);
}
static inline int fx_to_int(fixed32 fx) {
return fx / FIX_SCALE;
}
static inline float fx_to_float(fixed32 fx) {
return fx / FIX_SCALEF;
}
static inline fixed32 fx_multiply(fixed32 fa, fixed32 fb) {
return (fa*fb)>>FIX_SHIFT;
}
static inline fixed32 fx_division(fixed32 fa, fixed32 fb) {
return ((fa)*FIX_SCALE)/(fb);
}
Now I can change the affine parameter struct to use fixed-point numbers:
struct oam_affine_param {
u16 __filler1[3];
fixed16 pa;
u16 __filler2[3];
fixed16 pb;
u16 __filler3[3];
fixed16 pc;
u16 __filler4[3];
fixed16 pd;
} PK_AL(4);
And use them to set the identity matrix, so it's clear what's going on:
volatile struct oam_affine_param* main_affine = GetOAMAffinePointer(0);
main_affine->pa = main_affine->pd = fx_from_int(1);
main_affine->pb = main_affine->pc = 0;
Rotation and scaling
I'm not going to talk about the maths here, but here is my first function to rotate/scale a sprite:
void CalcRotationMatrix(volatile struct oam_affine_param* ptr, fixed32 angle, fixed32 scale) {
// Temporary slow calculation,
// to replace with lookup tables.
// [ pa pb ]
// [ pc pd ]
fixed32 calc_sin = fx_from_float(sinf(fx_to_float(angle)));
fixed32 calc_cos = fx_from_float(cosf(fx_to_float(angle)));
ptr->pa = fx_division(calc_cos, scale);
ptr->pb = fx_division(-calc_sin, scale);
ptr->pc = fx_division(calc_sin, scale);
ptr->pd = fx_division(calc_cos, scale);
}
And the code in the game loop to animate it:
fixed32 sin_counter = fx_from_float(sinf(fx_to_float(counter)));
CalcRotationMatrix(
main_affine,
counter,
fx_division(sin_counter, fx_from_int(2)) + fx_from_float(1.5)
);
Nice, it's all working. Now to sort out the fact that this is really slow.
As mentioned before, the GBA has no floating-point unit. This means that wherever I use sin/cos or even just adding floating-point numbers, GCC is making do with really slow software-based calculations, running every single frame.
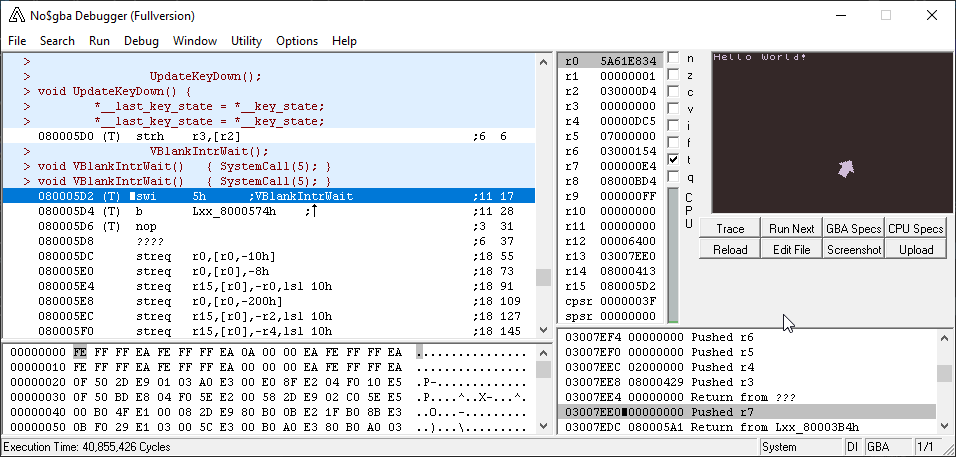
You can see this eating at my CPU budget in no$gba:
When that bar reaches the top, the GBA will run out of time before the next frame starts to draw, causing the game to lag. And I've already used a huge chunk of it just with this one sprite.
Lookup Tables
To combat this, I decided to work on a lookup table. An LUT it just a pre-computed array of values for my code to just look up instead of calculating everything on the fly.
I used Python to generate this:
import math, os
table_name = "sin_lut"
def function(index):
return math.sin(index)
count = 1024
fixed_point_size = 8
output_filename = table_name + ".c"
os.remove(output_filename)
with open(output_filename, "a") as f:
f.write(f"const short {table_name}[{count}] = {{\n")
column_count = 0
for i in range(0, count):
current_index = i*2*math.pi / count
calc = function(current_index)
fixedpoint = int(calc * 256)
if column_count == 0:
f.write(" ")
f.write(f"{hex(fixedpoint)}, ")
if column_count == 7:
column_count = 0
f.write("\n")
else:
column_count+=1
f.write("};")
It generates the following C code:
const short sin_lut[1024] = {
0x0, 0x1, 0x3, 0x4, 0x6, 0x7, 0x9, 0xa,
0xc, 0xe, 0xf, 0x11, 0x12, 0x14, 0x15, 0x17,
0x19, 0x1a, 0x1c, 0x1d, 0x1f, 0x20, 0x22, 0x24,
0x25, 0x27, 0x28, 0x2a, 0x2b, 0x2d, 0x2e, 0x30,
0x31, 0x33, 0x35, 0x36, 0x38, 0x39, 0x3b, 0x3c,
0x3e, 0x3f, 0x41, 0x42, 0x44, 0x45, 0x47, 0x48,
/*
...
*/
-0x31, -0x30, -0x2e, -0x2d, -0x2b, -0x2a, -0x28, -0x27,
-0x25, -0x24, -0x22, -0x20, -0x1f, -0x1d, -0x1c, -0x1a,
-0x19, -0x17, -0x15, -0x14, -0x12, -0x11, -0xf, -0xe,
-0xc, -0xa, -0x9, -0x7, -0x6, -0x4, -0x3, -0x1,
};
I can now just use this in my program! Because the array is const, it will be loaded into the cartridge ROM rather than taking up space in RAM.
To actually use this LUT, I made a new header file, trig.h:
#pragma once
#include "fixed.h"
#include "macros.h"
const fixed32 pi = 804;
const fixed32 tau = 1608;
extern const fixed32 sin_lut[1024];
INLINE fixed32 my_sine(fixed32 angle) {
u32 lookup = (angle * 512 / pi) & 0x3ff;
return sin_lut[lookup];
}
INLINE fixed32 my_cosine(fixed32 angle) {
return my_sine(angle + (pi / 2));
}
Thankfully, a cosine is the same as sine, just shifted up by pi/2. And who even uses tangent anyway.
I replaced all my slow code with this new function, and voila!
Performance issues are pretty much gone. I can't wait to use this to make some real fancy graphics!